RemoteFX Warning: You are currently using the RemoteFX 3D Video Adapter. ...
これが出たら、
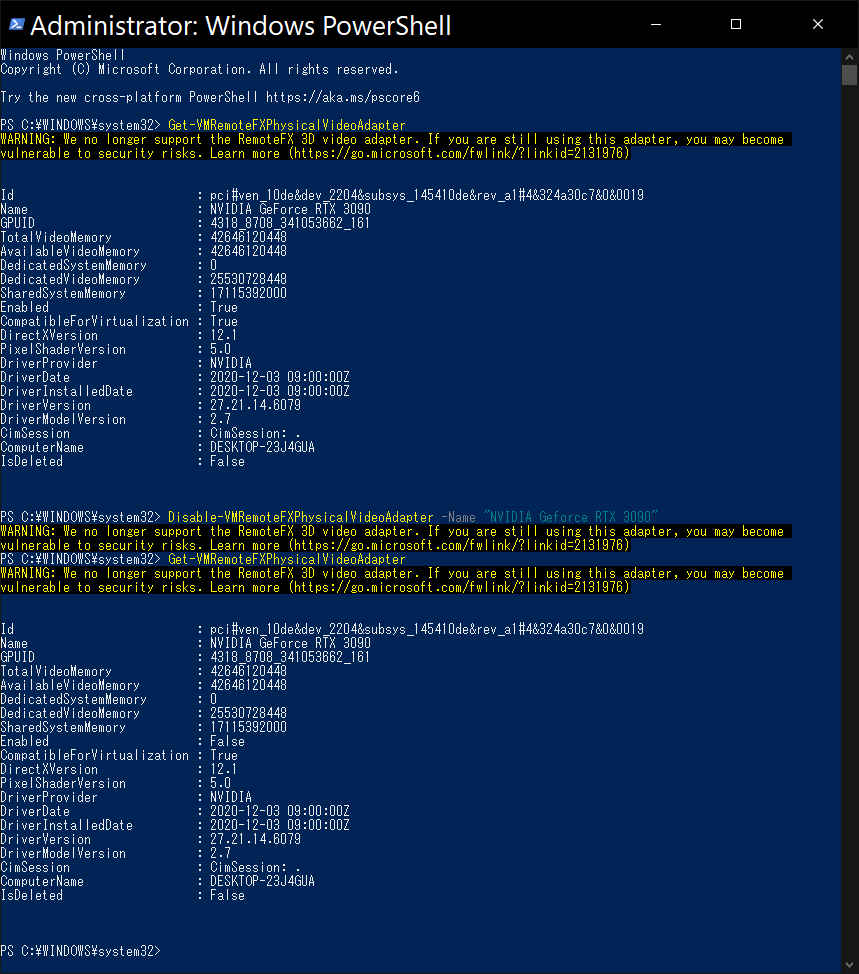
- 管理者権限で
powershellを実行 Get-VMRemoteFXPhysicalVideoAdapterコマンドでEnabledがTrueになっているデバイスのNameを確認Disable-VMRemoteFXPhysicalVideoAdapter -Name "NVIDIA Geforce RTX 3090"コマンドのように(2)で確認したNameを指定してデバイスの RemoteFX を無効化Get-VMRemoteFXPhysicalVideoAdapterコマンドでEnabledがFalseになったか確認
仕事中でもゲーム中でも突然に画面の真ん中に警告ダイアログが出てきて極めて邪魔です。OKを押すとしばらく出てこないので忘れてしまい、また突然邪魔される事態を繰り返す人も少なくなさそう。
トラックボールを Elecom M-DPT1MR から Kensington No. K72362JP Orbit Fusion へ替えて快適になったメモ
じみーにストレスになってたので替えました!いまのところ替えてよかったという印象が大きめです💕
新: Kensington No. K72362JP Orbit Fusion
よいところ
- 標準仕様で右クリックが薬指を前提とした位置のボタン!(人差し指と中指は玉の操作に専念できます!)
- スクロールリング使いやすい!(実際に使うまでどうなんだろう?って思ってました。使ってみたらこれはよいものです…)
- 第3ボタンがスクロールと独立していて押したい時にストレスなく押せる!(たいていのスクロールホイール方式の製品ではボタンを押したいのにスクロールしてもにょりが発生しやすいです)
- ボタンいっぱいある(5+DPI変更)
- 玉の大きさが大きい
- 支持球が人工ルビーで耐久性が高い(公式SPECには書いてないけど目視判断でたぶん人工ルビー。参考→ https://twitter.com/nekotrackball/status/1315996845152202753 )
- 玉の操作はとてもなめらか(持続性は長く使わないとわからない)
- 無線接続できる
- 電池がAA(調達性や他の電池機器との予備電池の共有が最も図りやすい)
- Kensignton なのにちゃんと右手操作に特化した設計(左右対称のっぺりは嫌なのです…分割キーボードの間に置いて使うとかならそれもいいのかもだけど)
わるい、とまでは言わないけれどちょっと残念なところ
- 有線で接続できない(電池の手間と重量が嫌なのです)
- スクロールリングを回す感触に軽いザラつきがある(操作に支障は無いけれど擦れ音と感触がチープで残念)
- 玉を外しにくい(お掃除のときちょっと気を使う)
旧: Elecom M-DPT1MR について
よいと感じていたところ
- 玉の大きさが大きい
- 玉の操作が人差し指&中指
- 支持球が人工ルビーで耐久性が高い(公式で人工ルビーと言ってる)
- 有線接続できる
- 無線接続もできる
- ボタンいっぱいある(5+3)
- なぜか5,000円前後で買える(メーカー希望小売価格は19,558円)
わるいところ (≈替えた理由)
- 標準仕様では右クリックが中指を前提とした位置のボタン
- 中指は人差し指とともに玉の操作に使いたいので右クリック時に指を一手間意識して動かす必要があった
- ハードウェア的に +3 のボタン部分は基本の 5 ボタンと違い、同じ割り当てをしても反応しないアプリがあったりして不便
- 薬指の位置のボタンもこの +3 部分なのでここに Left, Right, Center などの使用頻度の多いボタンを割り当てると動作しないアプリに遭遇してストレスになります
- Elecom Mouse Assistant っていう準ドライバーみたいな公式の常駐アプリを使う事でボタン設定はカスタマイズできるのだけど…これが絶妙に不便
- Windows を Sleep して復帰させると常駐はしていてもボタンのカスタマイズが解ける
- カスタマイズで割り当てた"右クリック"は一部のアプリでは効かない
- 一部のアプリの例がタスクマネージャーやリソースモニターだったりするのでつらい(右クリックしたい位置でキーボードのメニューキーを押すという技巧で操作する事はできる)
- カスタマイズを設定する画面でどの項目が実際どこのボタンなのか図が出ていてもわかりにくい(結果、適当な割り当てをしてどのボタンが実際にはどこで…と都度確認して設定していました)
- 不具合報告時のサポートの対応が悪かった
rust の wasm ターゲットのプロジェクトで surf-1.x を surf-2.x へ差し替える場合に必要な対応のメモ
surf-1.x 系では↓のように Cargo.toml にバージョン番号または所在だけ書けば wasm 向けにもそのまま使えました。べんり。
# surf-1.x [dependencies] surf = "1.0.3"
surf-2.x 系から↓のように Cargo.toml に default-features と features を明示的に設定しないと wasm ターゲットでビルドできなくなりました。
# surf-2.x
surf = {version = "2.1.0", default-features = false, features = ["wasm-client"]}
この設定を怠ると↓のようなエラーで依存 crates のビルド中に surf のビルドがエラーで失敗になります。
Compiling surf v2.1.0 error[E0432]: unresolved import `http_client::isahc` --> C:\Users\usagi\.cargo\registry\src\github.com-1ecc6299db9ec823\surf-2.1.0\src\client.rs:12:26 | 12 | use http_client::isahc::IsahcClient as DefaultClient; | ^^^^^ could not find `isahc` in `http_client` error: aborting due to previous error For more information about this error, try `rustc --explain E0432`. error: could not compile `surf`.
surf-2.0 のリリースノートによくみると wasm 向けには features を手設定しないとダメになるよって書いてある&wasm-test/Cargo.tomlを参考にするとわかります。READMEでどどーんとWASMで使いたければこの設定してねとは書かれていないので少し不親切かもしれません。のでメモを残しました。
`yarn licenses list --json` ではしんどい気配の場合に `npx license-checker --json` すると嬉しいメモ、とおまけで `Cargo.toml` で rust の場合のメモ
package.json -> licenses.json
package.json と npm|yarn を使っているプロジェクトでお世話になっている依存ライブラリーのライセンス表示を自動生成したい時、とりあえず yarn で
yarn licenses list --json
すると、↓しんどそうなJSON↓が出力される事があります。
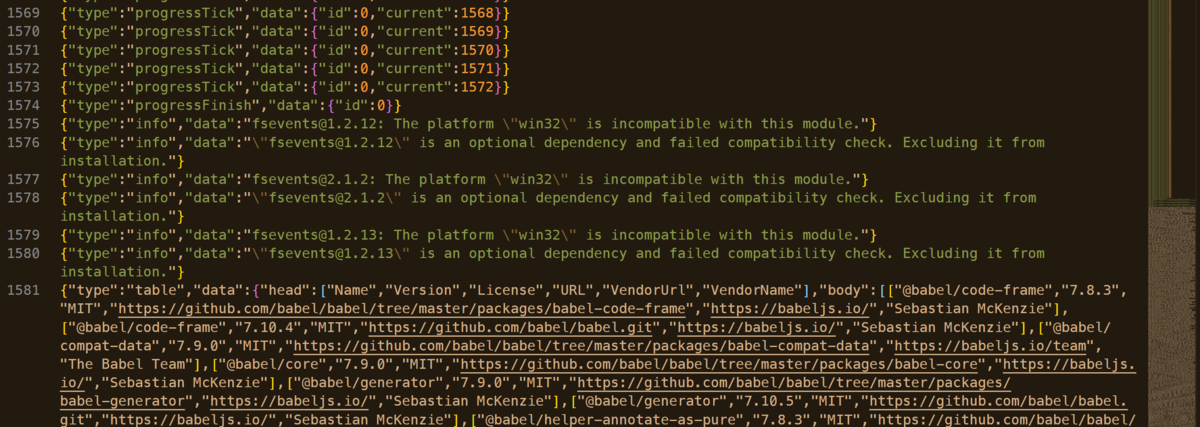
このときの1581行目は200,054文字ありました。 prettier も通らないし、しんどそうです。
そこで、
license-checkerhttps://www.npmjs.com/package/license-checker
に替えてみます:
npx license-checker --json --relativeLicensePath --summary
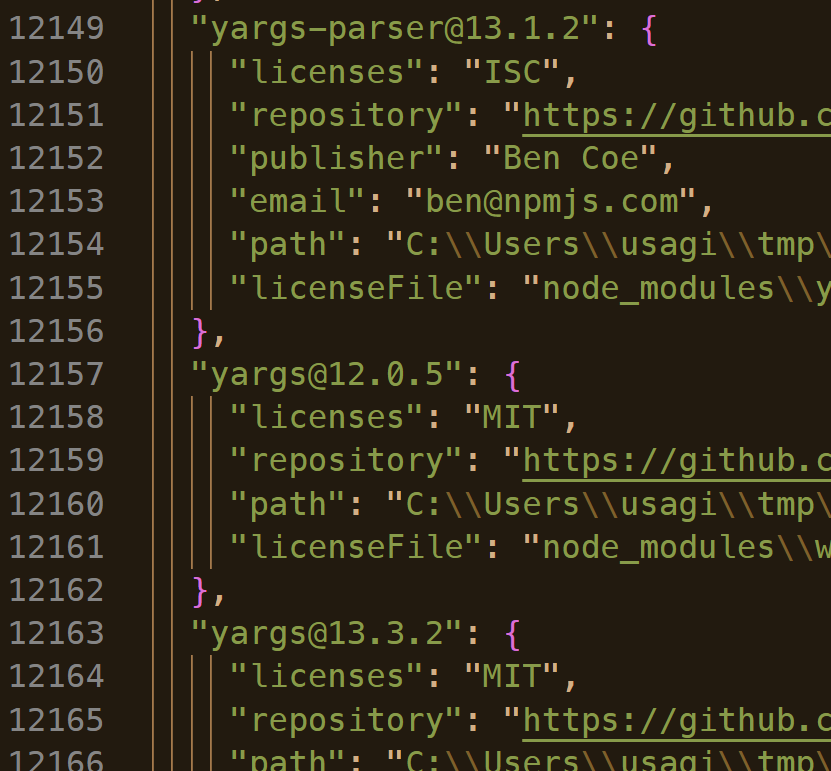
必要なところだけの出力が pretty されて得られました。この出力だと目視による部分的な確認も楽で、ライセンス表示の自動生成やプロジェクトの方針などで必要な場合にはGPLの混入防止検出なども問題なく処理できそうです。
おまけ: Cargo.toml -> licenses.json
cargo-licensehttps://github.com/onur/cargo-license
cargo install cargo-license
しておいて、
cargo-license -j
Rust の trait で Option<Self> や Result<Self, E> を return する関数を定義しようとして [E0277] で怒られた時に思い出すメモ
問題
// ↓これは問題ありません trait Trait { fn function() -> Self; } // ↓これは E0277: the size for values of type `Self` cannot be known at compilation time trait TraitOptional { fn function() -> Option<Self>; } // -> Result<Self, E> とかする場合も同様です(省略)
回避方法
// Self の代わりにジェネリクスを噛ませて trait TraitOptional<T> { fn function() -> Option<T>; } struct Struct{} // impl するときにジェネリクスの型引数に for と同じ型を渡す impl TraitOptional<Struct> for Struct { fn function() -> Option<Self> { Some( Self{} ) } }
Rust のメモリーコンテナー的な何かをわかりやすく整理したチートシートのメモ; T, Cell, RefCell, AtomicT, Mutex, RwLock, Rc, Arc

作ったので GitHub ↑ しつつ、なんとなくすごい久しぶりに Qiita に初心者さんに優しそうな雰囲気を装った解説↓
も書いてみました。ちなみに reddit ↓
にもポストしてみました。 reddit はとても参考になる議論がおおむね建設的にものすごい勢いで発生してくれるので嬉しいです。チートシートとしての意図と図面の都合による nitpick たちは README に注釈を付けるといいかなと思います。Allocationからの線の見直しなど a better なシートの提案はうまく取り込んで、できるだけウソの無い、でもチートシートの意図としてはわかりやすさを維持した調整をしたいと思います。
と、それだけ書いたのではわざわざブログにメモを残す理由が薄いので、ここには C++ と Rust でチートシートに掲載したメモリーコンテナー的なそれの大雑把なコードを、翻訳が通るソースとして書き残してみます。
おまけ: C++ の &≈ptr と (mutable)/const 系、Rust の &≈ptr と mut/const 系
// C++ #include <memory> #include <shared_mutex> #include <vector> #include <iostream> int main() { using T = int; using V = std::vector<T>; // mutable value T valm = 1; // const ref -> mutable value T& refc_valm = valm; refc_valm = 10; // const ref -> const value T const& refc_valc = valm; std::clog << refc_valc << " <- It's read only.\n"; // mutable ptr -> mutable value T* ptrm_valm = &valm; *ptrm_valm = 11; // const ptr -> mutable value T* const ptrc_valm = &valm; *ptrc_valm = 21; // const ptr -> const value const T* const ptrc_valc = &valm; std::clog << *ptrc_valc << " <- It's read only.\n"; // heap, ≈ 'static lifetime of Rust T* ptrm_heap_static_lifetime = new int(-1); // heap, ≈ mut Box<T> of Rust std::unique_ptr<T> ptrm_heap_single_owner_valm = std::make_unique<T>(-1); *ptrm_heap_single_owner_valm = -100; // heap, ≈ Box<T> of Rust std::unique_ptr<const T> ptrm_heap_single_owner_valc = std::make_unique<T>(-1); // heap, ≈ Rc<T> of Rust std::shared_ptr<const T> ptrm_heap_multiple_owner_thread_unsafe_valc = std::make_shared<T>(-1); // heap, ≈ Rc<Cell<T>> of Rust std::shared_ptr<T> ptrm_heap_multiple_owner_thread_unsafe_valm = std::make_shared<T>(-1); // heap, ≈ Rc<RefCell<V>> of Rust std::shared_ptr<V> ptrm_heap_multiple_owner_thread_unsafe_refm = std::make_shared<V>(V()); ptrm_heap_multiple_owner_thread_unsafe_refm->push_back(-2000); // single reader/writer control object, ≈ Mutex<T> without <T> of Rust std::mutex mutex_1rw_thread_safe_controller; // multiple reader/single writer control object, ≈ RwLock<T> without <T> of Rust std::shared_mutex mutex_mr1w_thread_safe_controller; }
// Rust; Rc:=Reference Counted, Arc:=Automatically Reference Counted use std:: { rc::Rc , sync::{Arc, Mutex, RwLock} , cell::{ Cell, RefCell } }; fn main() { type T = i32; type V = Vec<T>; // mutable value let mut valm: T = 1; let mut valm_the_other = 2; // const ref -> mutable value let refc_valm: &mut T = &mut valm; *refc_valm = 11; // const ptr -> const value let refc_valc: &T = &valm; println!("{} <-- It's a const value via const ref.", refc_valc); // mutable ptr -> mutable value; deref-ptr is an unsafe operation let mut ptrm_valm: *mut T = &mut valm as *mut T; unsafe { *ptrm_valm = 21 }; ptrm_valm = &mut valm_the_other as &mut T; unsafe { *ptrm_valm = 22 }; // const ptr -> mutable value let ptrc_valm: *mut T = &mut valm as *mut i32; unsafe { *ptrc_valm = 31 }; // const ptr -> const value let ptrc_valc: *const T = &valm as *const i32; println!("{:?} <-- It's a const value via const ptr.", ptrc_valc); // heap, ≈ new of C++ let mut ptrm_heap_static_lifetime: *mut T = unsafe{ std::alloc::alloc( std::alloc::Layout::new::<T>() ) } as *mut T; unsafe { *ptrm_heap_static_lifetime = -10 }; // heap, ≈ std::unique_ptr<T> of C++, deref -> mutable value let mut ptrm_heap_single_owner_valm: Box<T> = Box::<T>::new(-1); *ptrm_heap_single_owner_valm = -100; // heap, ≈ std::unique_ptr<const T> of C++, deref -> mutable value let ptrm_heap_single_owner_valc: Box<T> = Box::<T>::new(-1); // heap, ≈ std::shared_ptr<const T> of C++, deref -> const value let ptrm_heap_multiple_owner_thread_unsafe_valc: Rc<T> = Rc::<T>::new(-1); // heap, ≈ std::shared_ptr<T> + std::mutex of C++, deref -> mutable value let ptrm_heap_multiple_owner_thread_unsafe_valm: Rc<Cell<T>> = Rc::new(Cell::<T>::new(-1)); ptrm_heap_multiple_owner_thread_unsafe_valm.set( -200 ); // heap, ≈ std::shared_ptr<T> + std::mutex of C++, deref -> mutable ref let ptrm_heap_multiple_owner_thread_unsafe_refm: Rc<RefCell<V>> = Rc::new(RefCell::new(V::new())); ptrm_heap_multiple_owner_thread_unsafe_refm.borrow_mut().push( -2000 ); // heap, ≈ std::shared_ptr<const T> of C++, deref -> const value let ptrm_heap_multiple_owner_thread_unsafe_valc: Arc<T> = Arc::<T>::new(-1); // heap, ≈ std::shared_ptr<T> + std::shared_mutex of C++, deref -> mutable value let ptrm_heap_multiple_owner_thread_unsafe_valm: Arc<Mutex<T>> = Arc::new(Mutex::<T>::new(-1)); *ptrm_heap_multiple_owner_thread_unsafe_valm.lock().unwrap() = -200; // heap, ≈ std::shared_ptr<T> + std::shared_mutex of C++, deref -> mutable ref let ptrm_heap_multiple_owner_thread_unsafe_refm: Arc<RwLock<T>> = Arc::new(RwLock::<T>::new(-1)); { let r0 = *ptrm_heap_multiple_owner_thread_unsafe_refm.read().unwrap(); let r1 = *ptrm_heap_multiple_owner_thread_unsafe_refm.read().unwrap(); println!("r0 = {:?}, r1 = {:?}", r0, r1); // drop(≈release) r0, r1 then it will be writable in the out of this scope } *ptrm_heap_multiple_owner_thread_unsafe_refm.write().unwrap() = -3000; }
参考
- rust — Rustのセルと参照カウントタイプについての全体的な説明が必要
- Unsafe Rust - The Rust Programming Language
- RefCell<T>と内部可変性パターン - The Rust Programming Language
- Arc<Mutex<T>>という形はデザインパターン - Rustコトハジメ
- brughdiggity comments on Hey Rustaceans! Got an easy question? Ask here (22/2017)!
- Explicate what "Rc" and "Arc" stand for. by ucarion · Pull Request #42419 · rust-lang/rust · GitHub
- Rust RefCell(T) - javatpoint
- Rust book 勉強会 #7 - slideship.com
Rust で実行中にバッファーの次元解釈を変更できる DimensionShiftableBuffer と翻訳時に任意の次元解釈をVec<T>に追加する vec-dimension-shift を公開しました。のメモ
- dimension_shift_buffer
- vec-dimension-shift
前提として、どちらも単一のヒープに全体が連続したメモリーアドレスを持つバッファーを扱う、という事があります。そのうえで、バッファーを任意次元に再解釈します。
dimension_shiftable_buffer
実行時に任意の次元にバッファーの解釈を変更したビューを用いてバッファーを扱える、そういうものです。こちらの実装はすべて Safe です。 unsafe せずに Vec<T> を実行時に任意次元へ再解釈する方法は思いつかなかったので getter(get,pop,remove)/setter(push,append) と for_each を用意しました。こちらの利点は「実行時に」「任意次元へ」です。
// make a 2d-empty DimensionShiftableBuffer let mut dsb = DimensionShiftableBuffer::<u8>::new(vec![], 2).unwrap(); // push a 2d-datum dsb.push(&[0u8, 1]).unwrap(); // push a 2d-datum dsb.push(&[2u8, 3]).unwrap(); // append a 2d-datum sequence dsb.append(&[4u8, 5, 6, 7, 8, 9, 10, 11]).unwrap(); for index in 0..dsb.len().unwrap() { // get a 2d slice assert_eq!(dsb.get(index).unwrap(), &[index as u8 * 2, index as u8 * 2 + 1]); } // shift dimension to 3 from 2 dsb.shift_dimension(3).unwrap(); // push a 3d-datum dsb.push(&[12u8, 13, 14]).unwrap(); // get a 3d-datum assert_eq!(dsb.get(0).unwrap(), &[0u8, 1, 2]); assert_eq!(dsb.get(1).unwrap(), &[3u8, 4, 5]); assert_eq!(dsb.get(2).unwrap(), &[6u8, 7, 8]); assert_eq!(dsb.get(3).unwrap(), &[9u8, 10, 11]); assert_eq!(dsb.get(4).unwrap(), &[12u8, 13, 14]); // get a linear slice let linear_slice = dsb.as_slice(); assert_eq!(linear_slice, &[0u8, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]);
vec-dimension-shift
こちらは翻訳時にN次元から実際に対応する具体的な次元の次元再解釈機能を選択的に Vec<T> へ付与する trait 集です。 usize 次元のすべてのパターンを lib に埋め尽くすわけにはいかないので、2..16次元は features で選択的に使用可能に、 default で 2,3,4 次元の traits を定義としつつ、 make_vec_dimension_shift_n_dimension! マクロをユーザーが任意に呼べるように pub り、 crate のユーザーが任意に欲しい次元を選択的に扱えるようにしています。
こっちの中身は黒魔術と unsafe でできています。次元再解釈時の境界チェック、直接の変換が不可能な場合のErr|truncate|paddingなど基本的には安全に使いやすいように実装していますが、N次元から1次元化するための flatten の実装では Vec の実装とメモリーレイアウトをにゃーんしたりしていたりします。
use vec_dimension_shift::{ VecDimensionShift2D, VecDimensionShift2DFlatten, VecDimensionShift3D, VecDimensionShift3DFlatten }; fn d2_and_d3() { let original = vec![0.0, 1.1, 2.2, 3.3, 4.4, 5.5]; dbg!(&original); let mut d2_shifted = original.as_2d_array().unwrap(); dbg!(&d2_shifted); assert_eq!(d2_shifted[0], [0.0, 1.1]); assert_eq!(d2_shifted[1], [2.2, 3.3]); assert_eq!(d2_shifted[2], [4.4, 5.5]); d2_shifted[1][1] = -1.0; let flatten = d2_shifted.as_flatten(); dbg!(&flatten); let mut d3_shifted = flatten.as_3d_array().unwrap(); dbg!(&d3_shifted); assert_eq!(d3_shifted[0], [0.0, 1.1, 2.2]); assert_eq!(d3_shifted[1], [-1.0, 4.4, 5.5]); d3_shifted[1][1] = -2.0; let flatten = d3_shifted.as_flatten(); dbg!(&flatten); assert_eq!(flatten, vec![0.0, 1.1, 2.2, -1.0, -2.0, 5.5]) }
ちなみに、 1D -> 2D とした後に 1D へ flattening せず、 1D -> 2D -> 3D と次元再解釈すると、
use vec_dimension_shift::make_vec_dimension_shift_n_dimension; fn n_dimension_macro_generator() { make_vec_dimension_shift_n_dimension! { VecDimensionShift2D, VecDimensionShift2DFlatten, as_2d_array_no_check, to_2d_array_no_check, as_2d_array, to_2d_array, as_2d_array_truncate, to_2d_array_truncate, as_2d_array_padding, to_2d_array_padding, 2 } make_vec_dimension_shift_n_dimension! { VecDimensionShift3D, VecDimensionShift3DFlatten, as_3d_array_no_check, to_3d_array_no_check, as_3d_array, to_3d_array, as_3d_array_truncate, to_3d_array_truncate, as_3d_array_padding, to_3d_array_padding, 3 } let original = vec![0.0, 1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9, 10.10, 11.11]; dbg!(&original); let d2 = original.as_2d_array().unwrap(); assert_eq!(d2[0], [0.0, 1.1]); assert_eq!(d2[1], [2.2, 3.3]); assert_eq!(d2[2], [4.4, 5.5]); assert_eq!(d2[3], [6.6, 7.7]); assert_eq!(d2[4], [8.8, 9.9]); assert_eq!(d2[5], [10.10, 11.11]); dbg!(&d2); let d3 = d2.as_3d_array().unwrap(); assert_eq!(d3[0], [[0.0, 1.1], [2.2, 3.3], [4.4, 5.5]]); assert_eq!(d3[1], [[6.6, 7.7], [8.8, 9.9], [10.10, 11.11]]); dbg!(&d3); }
こういう多N次元(N次元×N次元×…)も作れます。

